Porovnání s konkurencí
Jelikož přinášíme komplexní matematickou aplikaci, pak naší konkurencí jsou nejen matematické aplikace typu Photomath, Mathway, Microsoft Math a další, ale také velké jazykové modely LLM. Výhody oproti LLM shrnujeme v sekci o slovních úlohách. Zde se zaměříme na porovnání čistě matematických schopností aplikace a srovnáme naše řešení s nejznámější aplikací Photomath.✱ Datum porovnání: únor 2025
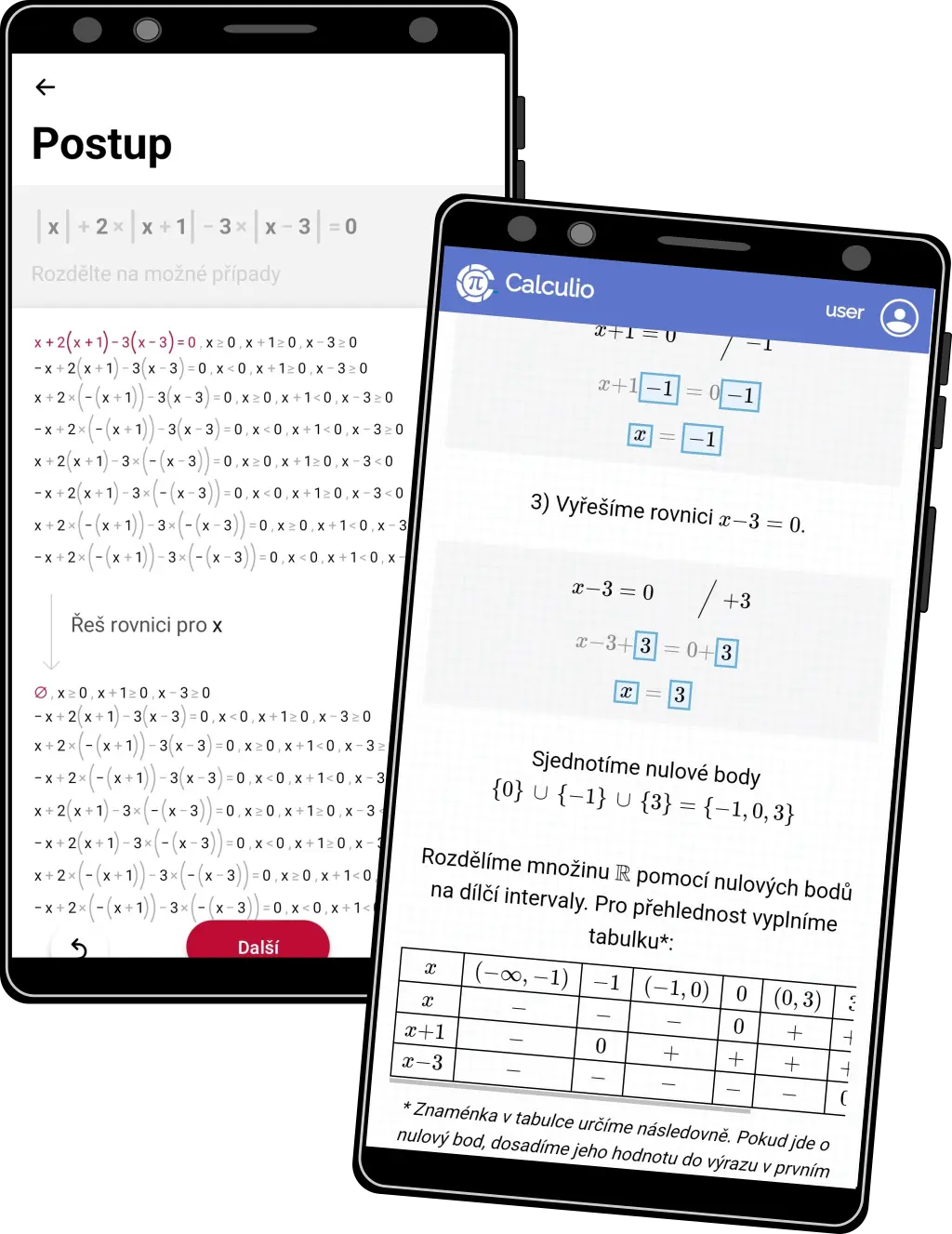
Elegantní řešení #1
- Používáme běžně zažité metody jako například metodu nulových bodů
- Tuto metodu využíváme nejen u rovnic a nerovnic s absolutní hodnotou, ale také u složitějších rovnic/nerovnic v součinovém či podílovém tvaru.
- Výsledné řešení je pak mnohem přehlednější a srozumitelnější.
- Zahrnujeme všechny kroky (nic nevynecháváme na rozdíl od jiných aplikací)
- Nemusíte se složitě rozklikávat hlouběji a hlouběji, jediný případný rozklik je na modrý obdélník pro detailnější vysvětlení daného kroku.
- Různé části rovnice řešíme paralelně stejně jako to dělá člověk. To znamená, že neupravujeme nejprve jednu složitější část, pak druhou apod.
- Na obrázku vlevo Photomath, vpravo Calculio
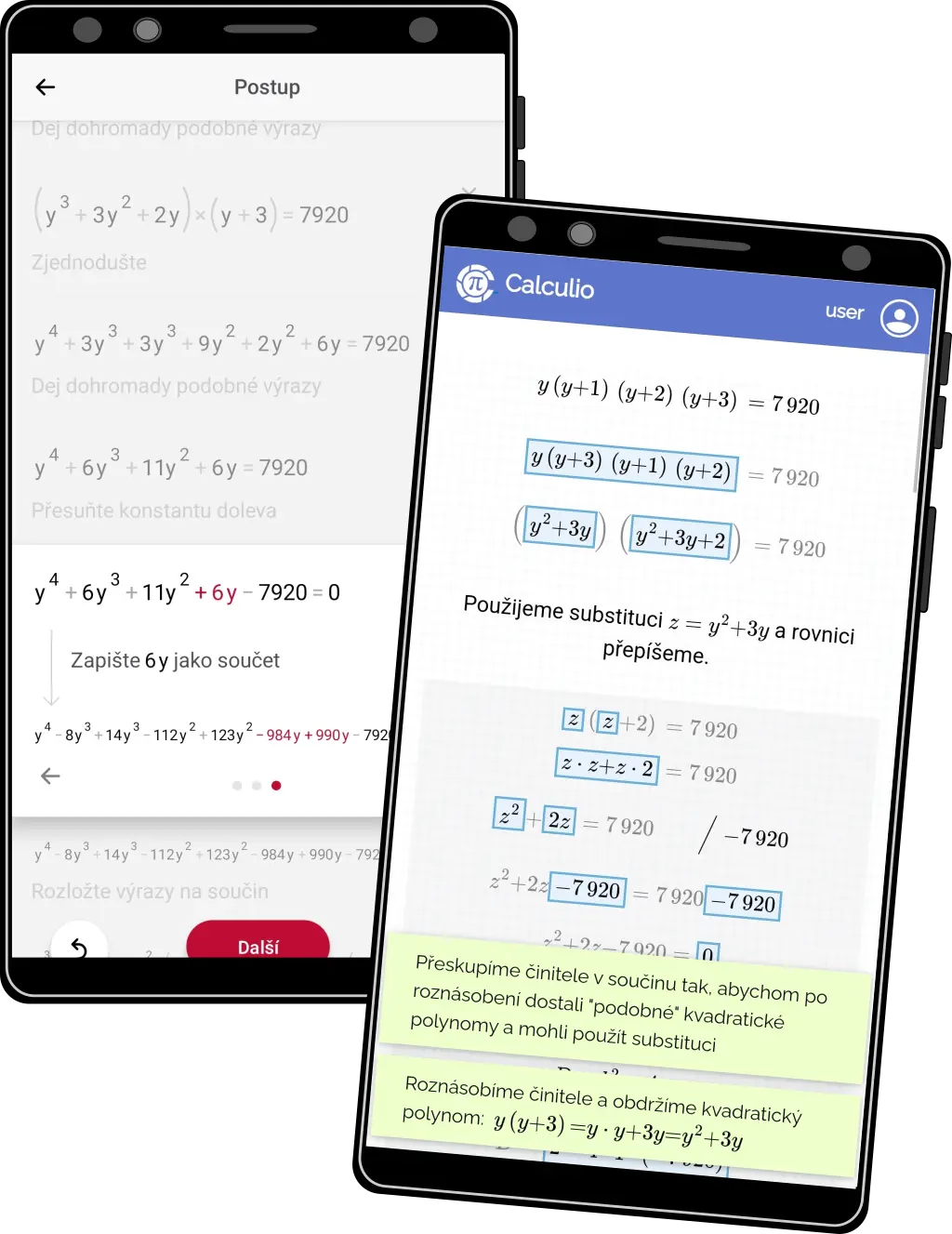
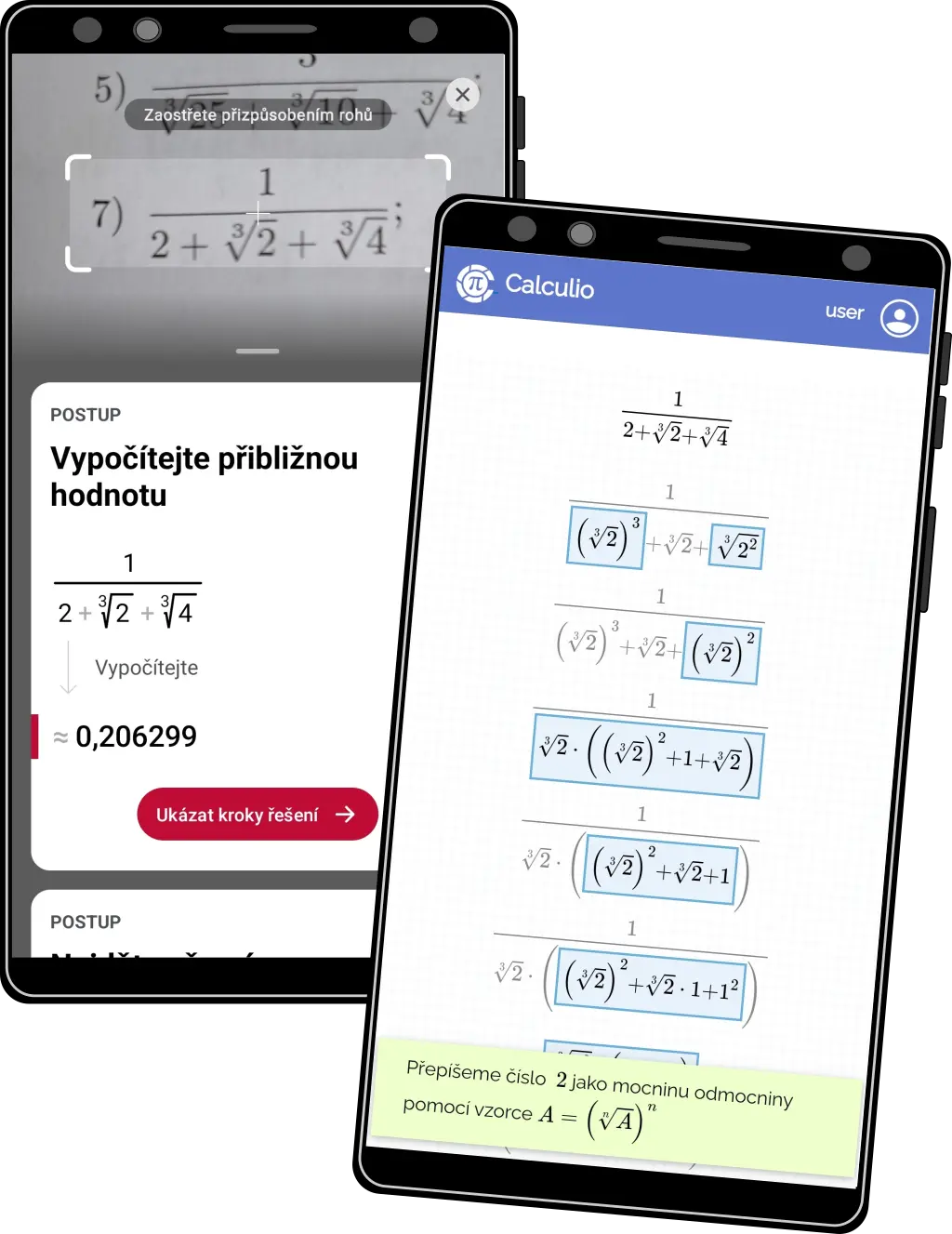
Elegantní řešení #2
- Hledáme elegantní, chytré řešení namísto "utlučení" hrubou silou
- Povšimněte si, že namísto roznásobení všech závorek nejprve vhodně činitel přeskupíme a sloučíme, vystačíme si pak s obyčejnou kvadratickou rovnicí
- Pokud nevíte proč 6y přepsat na součet -984y + 990y, tak je to jen proto, aby konkurence mohla kvartickou rovnici (kterou si sama vyrobila) rozložit na součin. K tomuto rozkladu přišla numerickými metodami bez jakéhokoliv vysvětlení a pro studenta bez šance samostatně vypočítat analogický příklad
- Na obrázku vlevo Photomath, vpravo Calculio
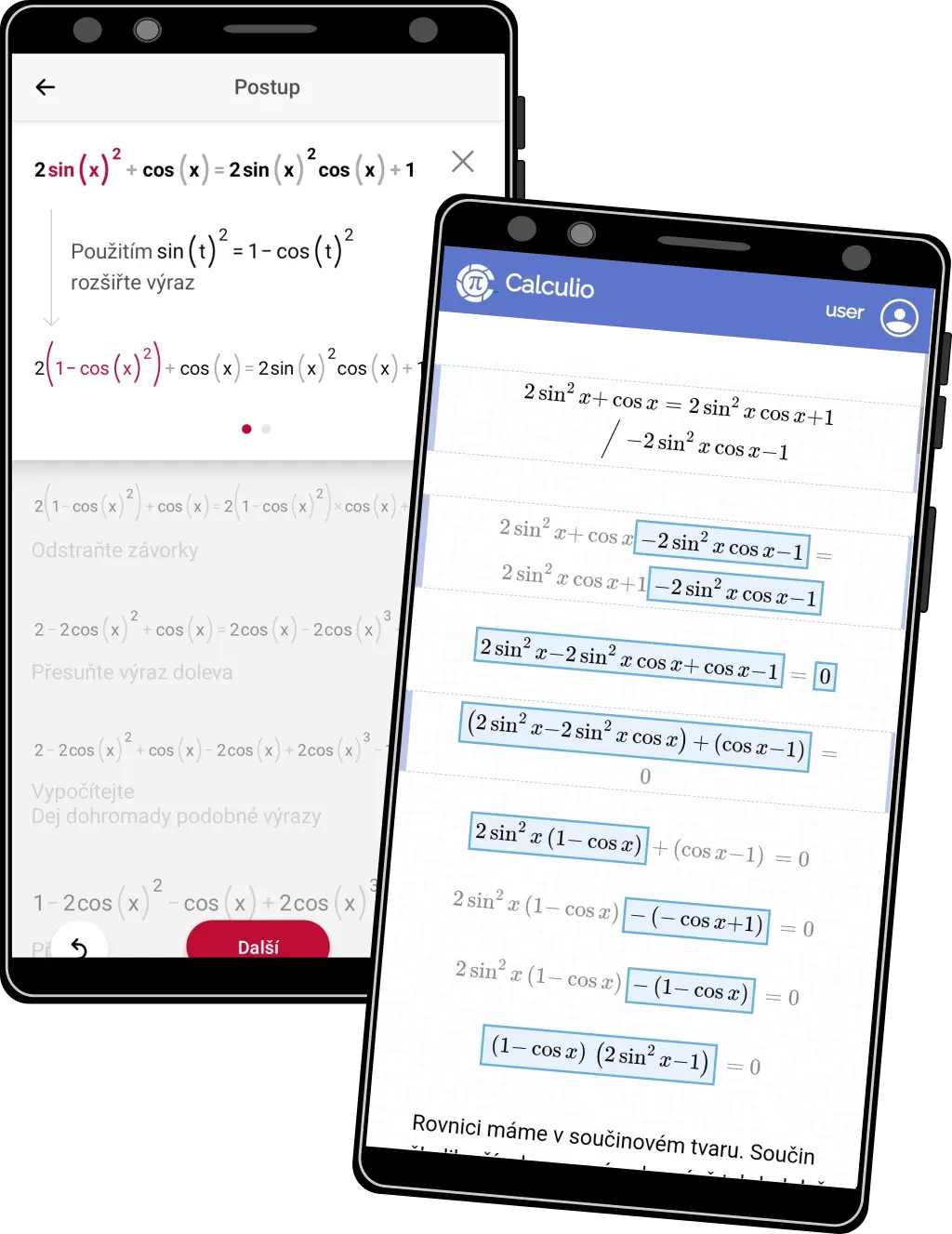
Elegantní řešení #3
- Neděláme zbytečné operace/úkony pokud nejsou zapotřebí
- Například není zapotřebí přepisovat mocninu sinu pomocí vzorce. Je to naprosto zbytečný krok, který jen komplikuje a prodlužuje celý postup.
- Na obrázku vlevo Photomath, vpravo Calculio
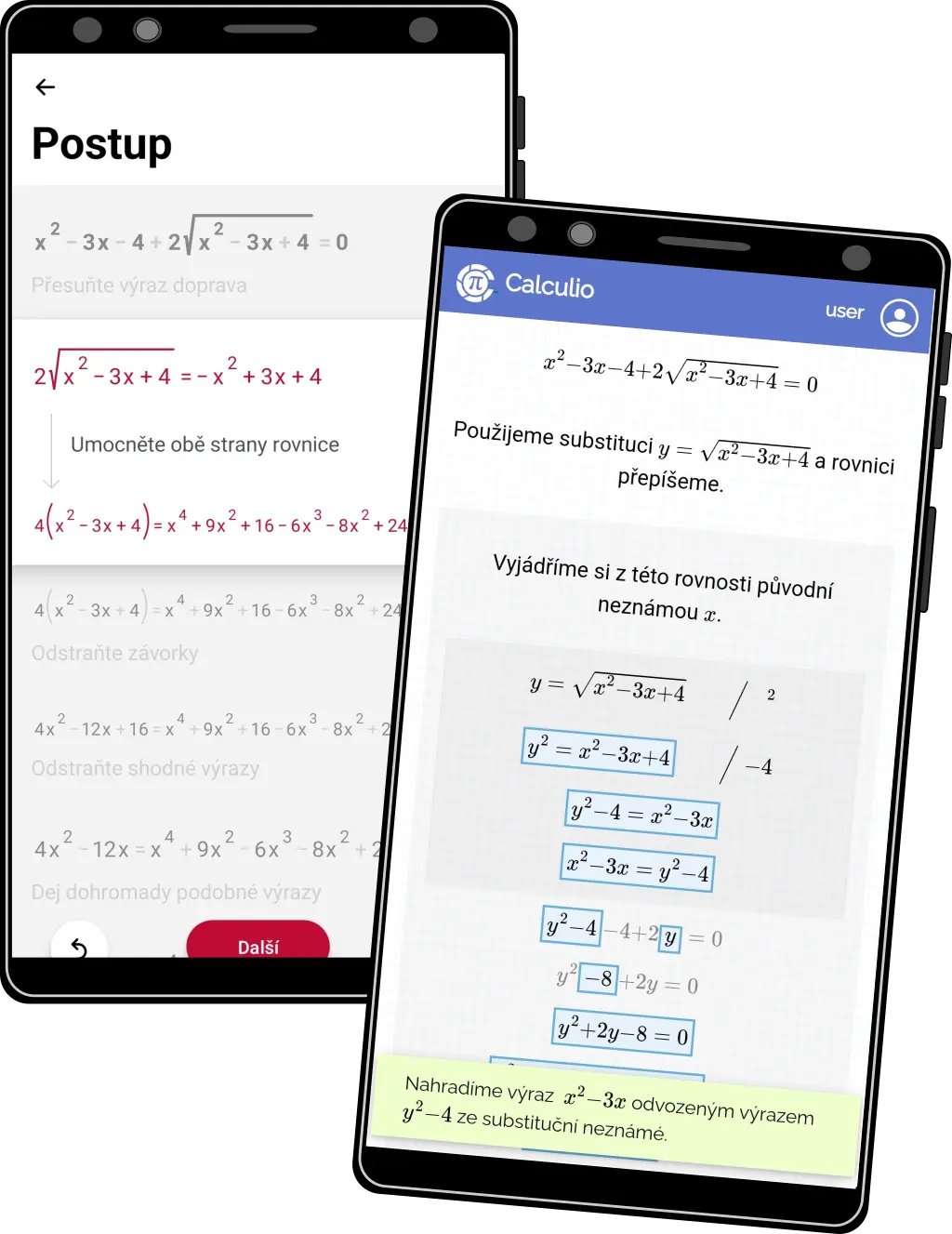
Chytrá substituce
- Implementujeme mnoho způsobů, jak uplatnit a aplikovat substituční metodu
- Výsledné řešení je zpravidla přehlednější a jednodušší
- Student si pak vystačí se základními metodami jako je kvadratická rovnice, namísto toho aby řešil kubické nebo kvartické rovnice, které často ani řešit nelze mimo numerických metod.
- Na obrázku vlevo Photomath, vpravo Calculio
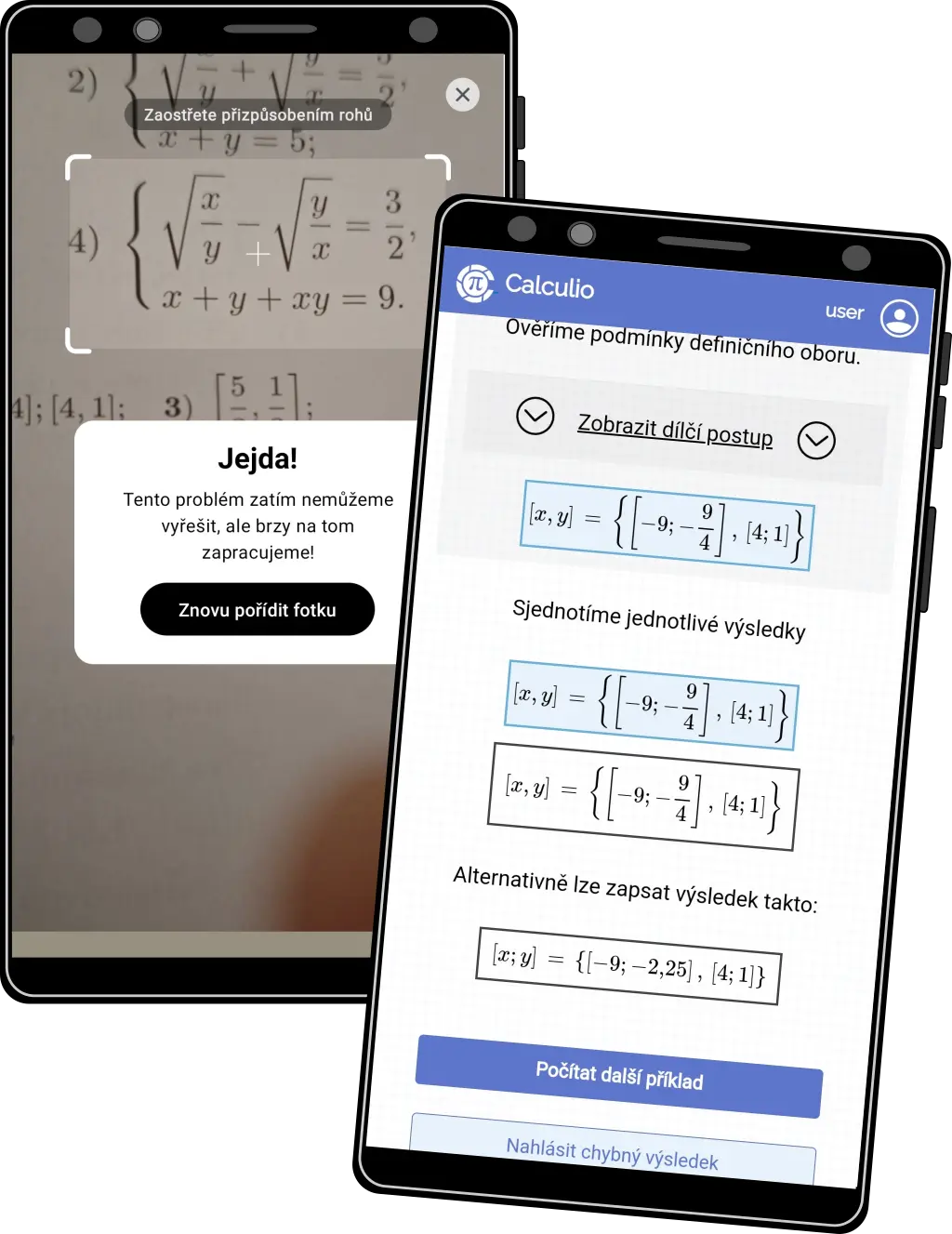
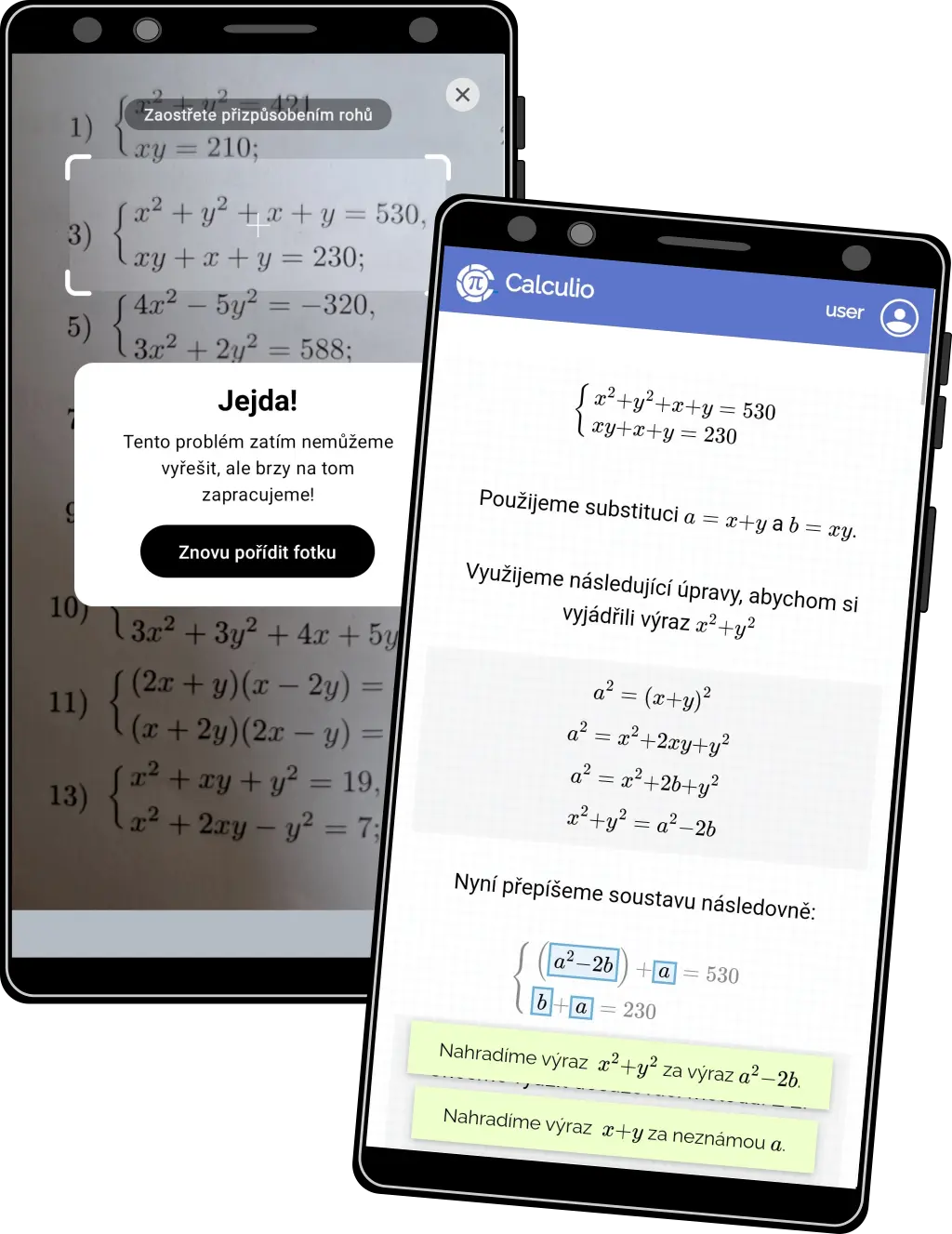
Soustavy rovnic #1
- Díky sofistikovaným metodám zvládáme i složitější soustavy rovnic, na které konkurence již nestačí
- V tomto případě lze využít substituci pro zjištění vztahu mezi neznámými z první rovnice a poté tento vztah doplnit do druhé rovnice
- Na obrázku vlevo Photomath, vpravo Calculio
Soustavy rovnic #2
- Implementuje i běžné tipy a triky při řešení soustav.
- Vše je do posledního detailu vysvětleno tak, aby to student pochopil a mohl sám aplikovat na analogickém příkladu.
- Na obrázku vlevo Photomath, vpravo Calculio
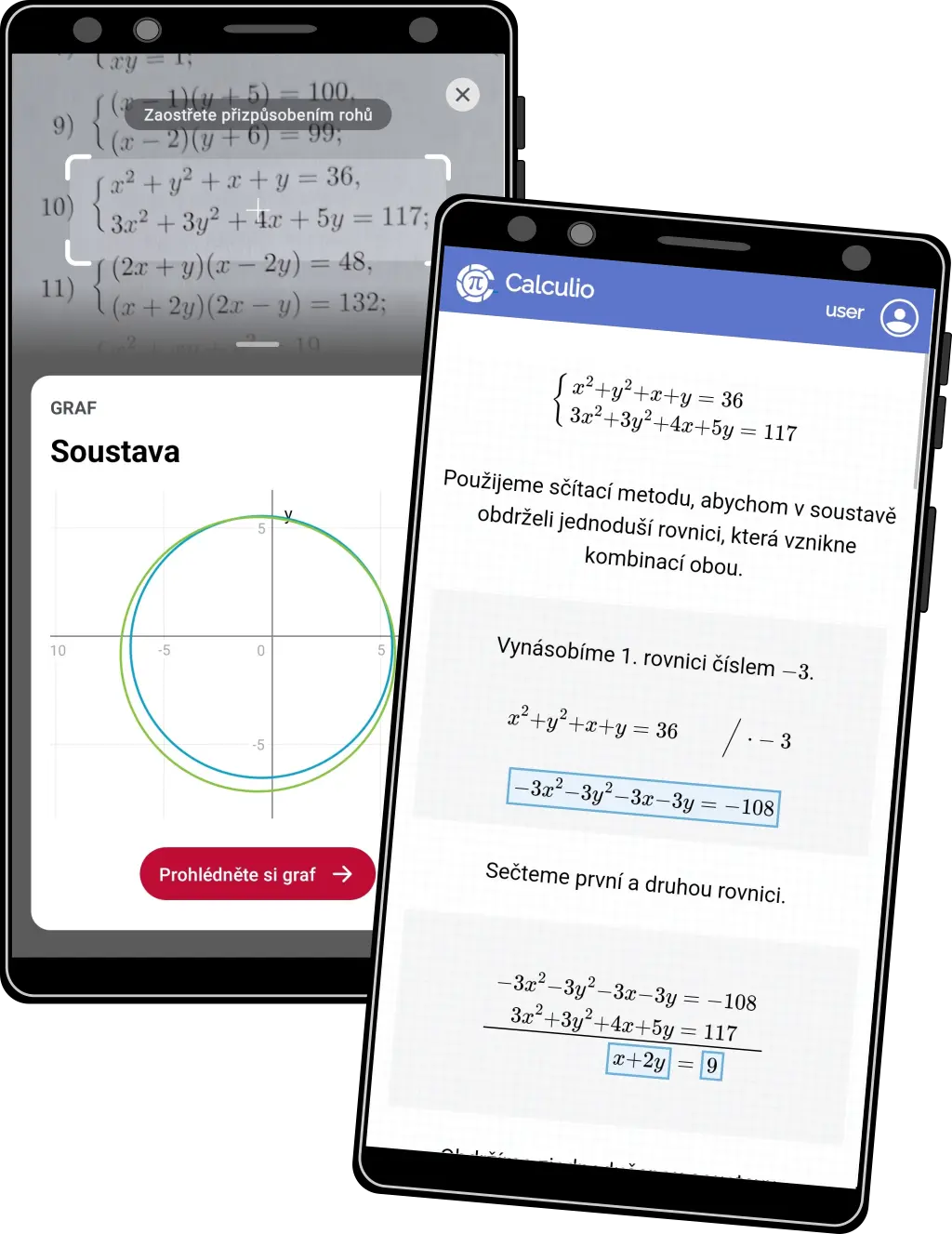
Soustavy rovnic #3
- Někdy pro složitě vypadající soustavy stačí využít elementární postupy jak je například sčítací metoda
- Soustava se pak velmi rychle redukuje na o dost jednodušší soustavu
- Na obrázku vlevo Photomath, vpravo Calculio
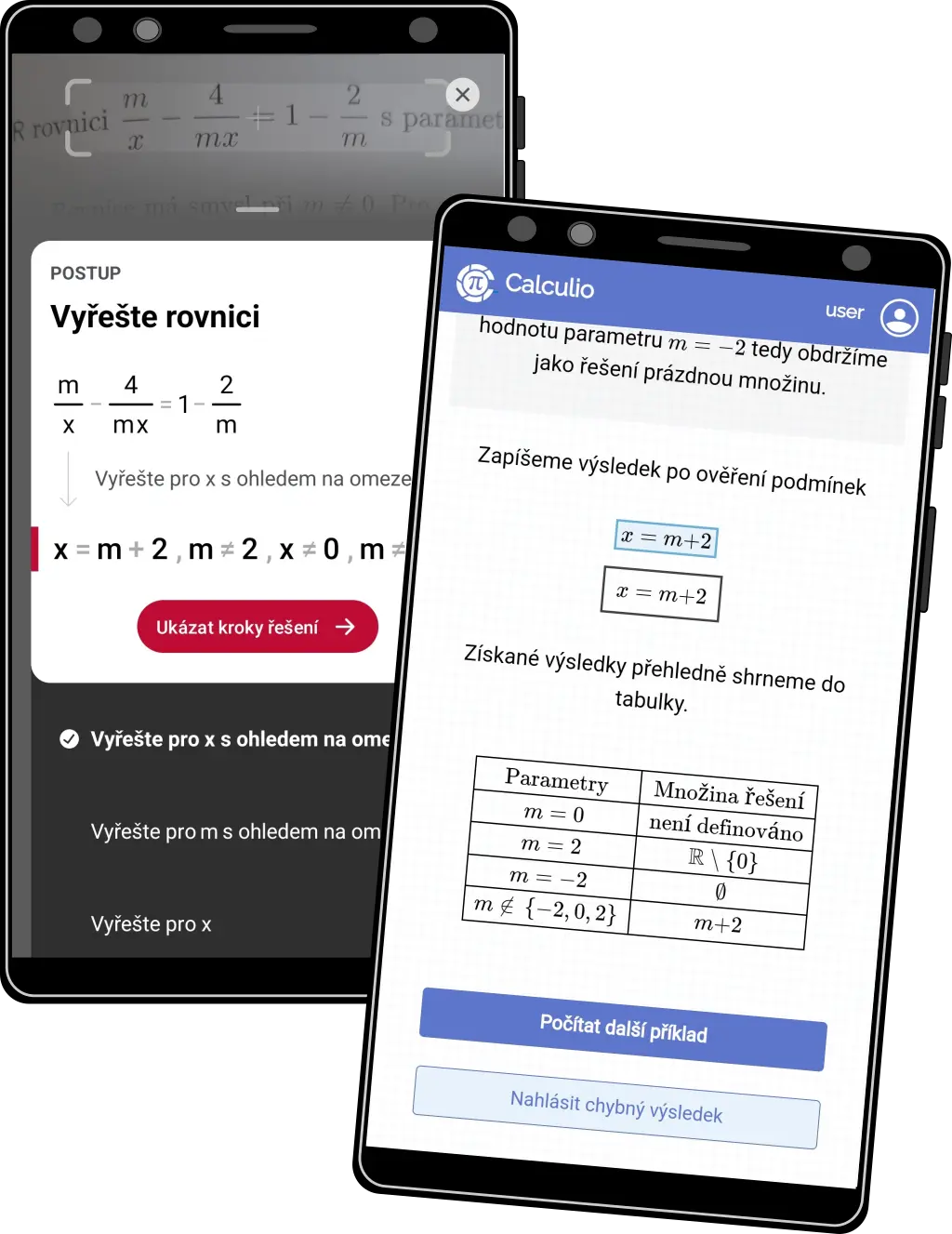
Rovnice a nerovnice s parametry
- Calculio je jediná aplikace na světě, která toto téma zvládá.
-
Ostatní aplikace se chovají následovně:
- Řešení nedodají vůbec
- Poskytnou jen výsledek (často nekompletní či nesprávný) bez jakéhokoli postupu
- Poskytnou jen vyjádření neznámé bez jakéhokoli vyšetření krajních případů, ošetření podmínek apod.
- Na konci příkladu poskytujeme přehledné shrnutí v diskuzní tabulce
- Na obrázku vlevo Photomath, vpravo Calculio
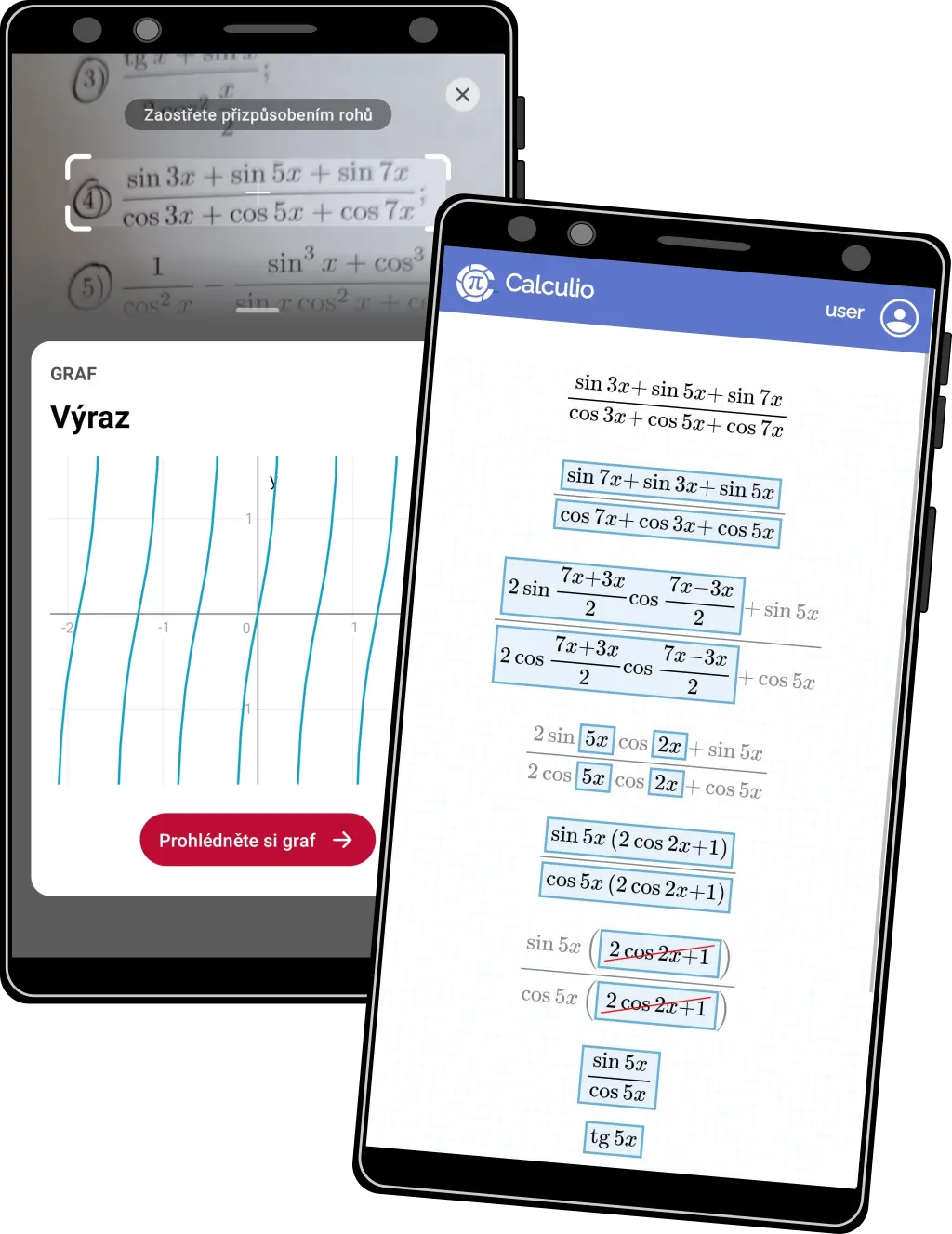
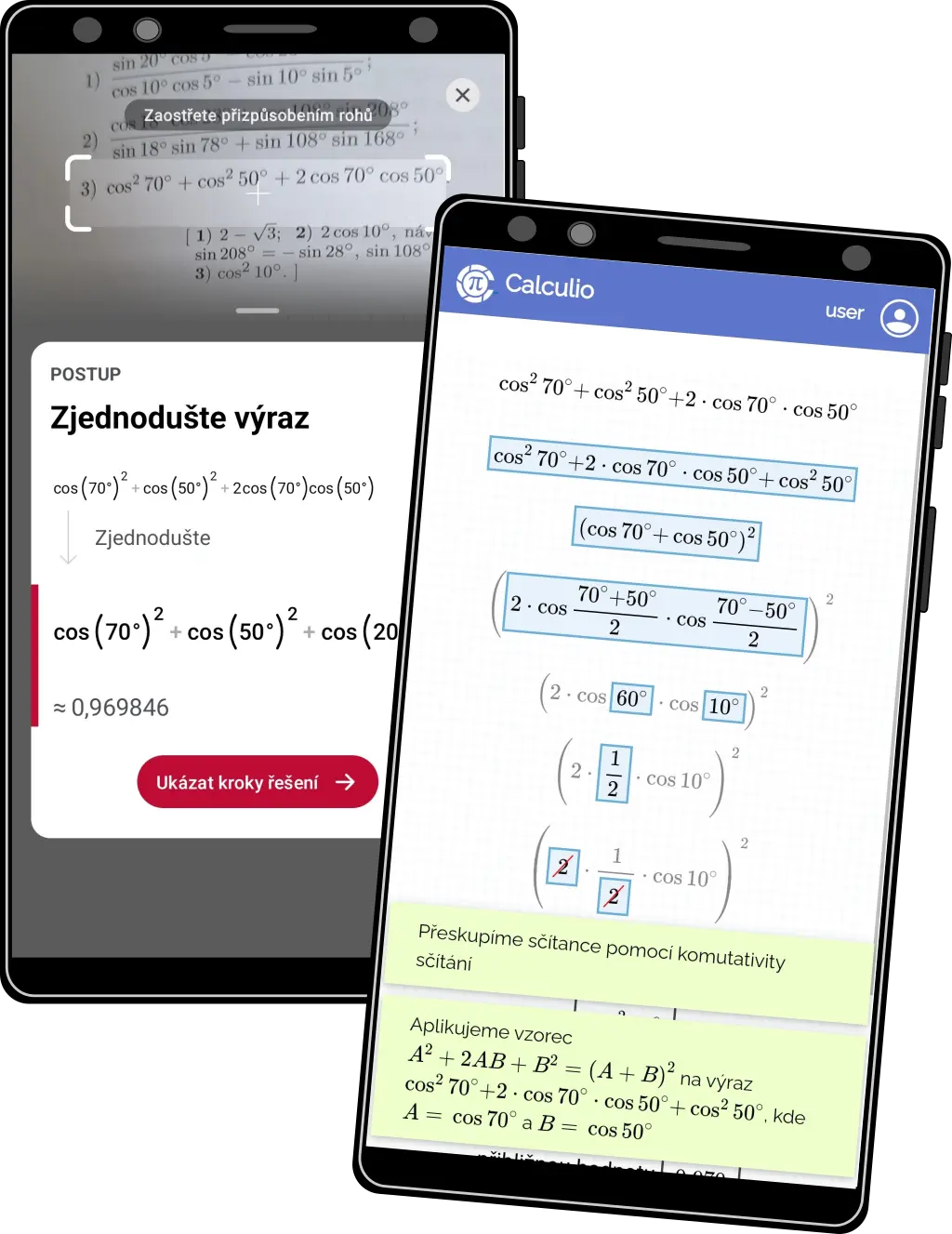
Goniometrické výrazy
- Pro studenty je úprava goniometrických výrazů často složitým tématem díky existenci velkého počtu vzorečků, vztahů a hodnot.
- Dokážeme vysvětlit zjednodušení goniometrického výrazu tak, aby to student pochopil a nedělal při tom složité a kostrbaté (a často zbytečné) kroky
- Na obrázku vlevo Photomath, vpravo Calculio
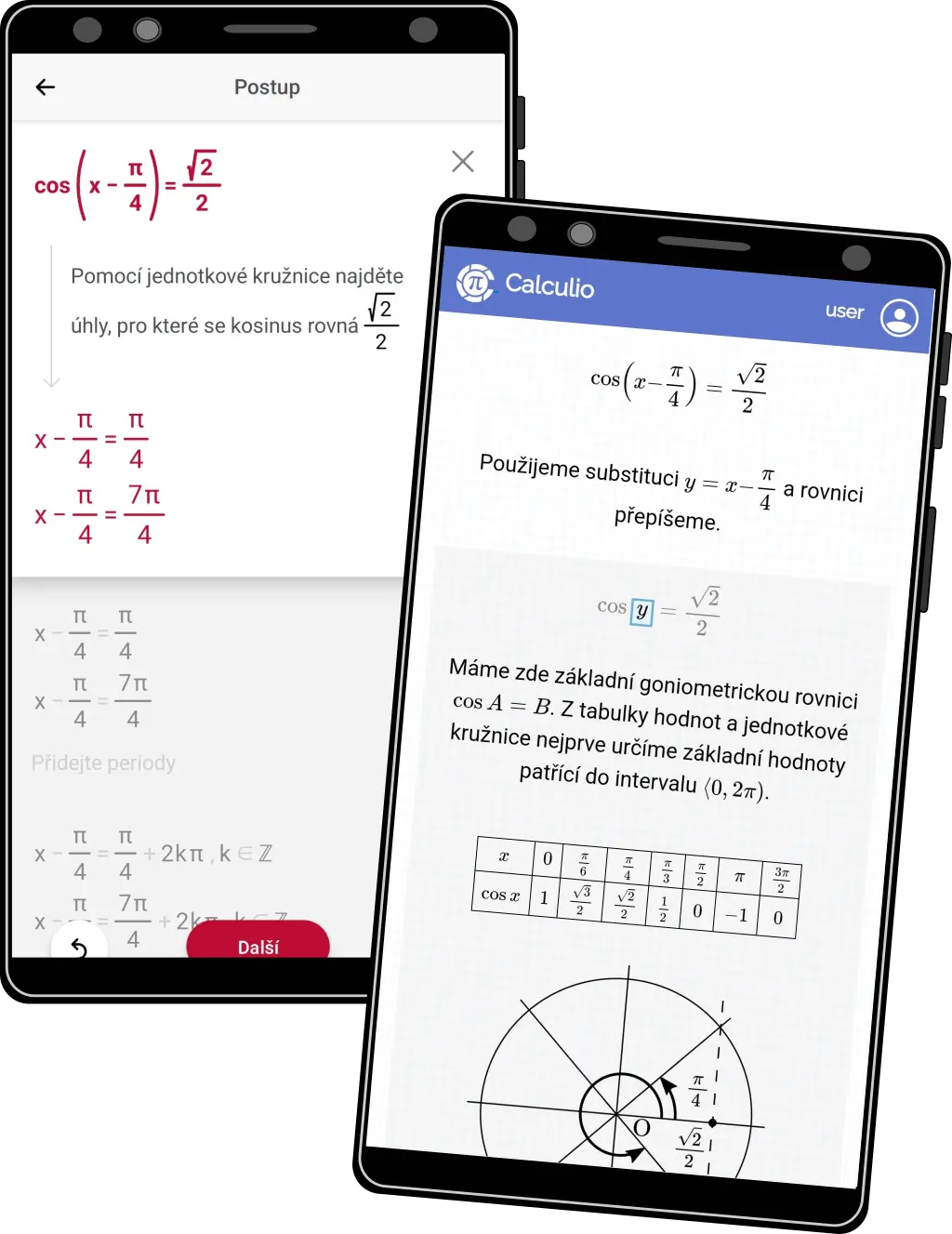
Goniometrické rovnice
- Přidáváme grafické znázornění jednotkové kružnice tak, aby byl postup přehlednější a jasnější.
- Řešení pak je vizuálně k nerozeznání od postupů v učebnicích, jen je většinou detailnější pro lepší pochopení.
- Na obrázku vlevo Photomath, vpravo Calculio
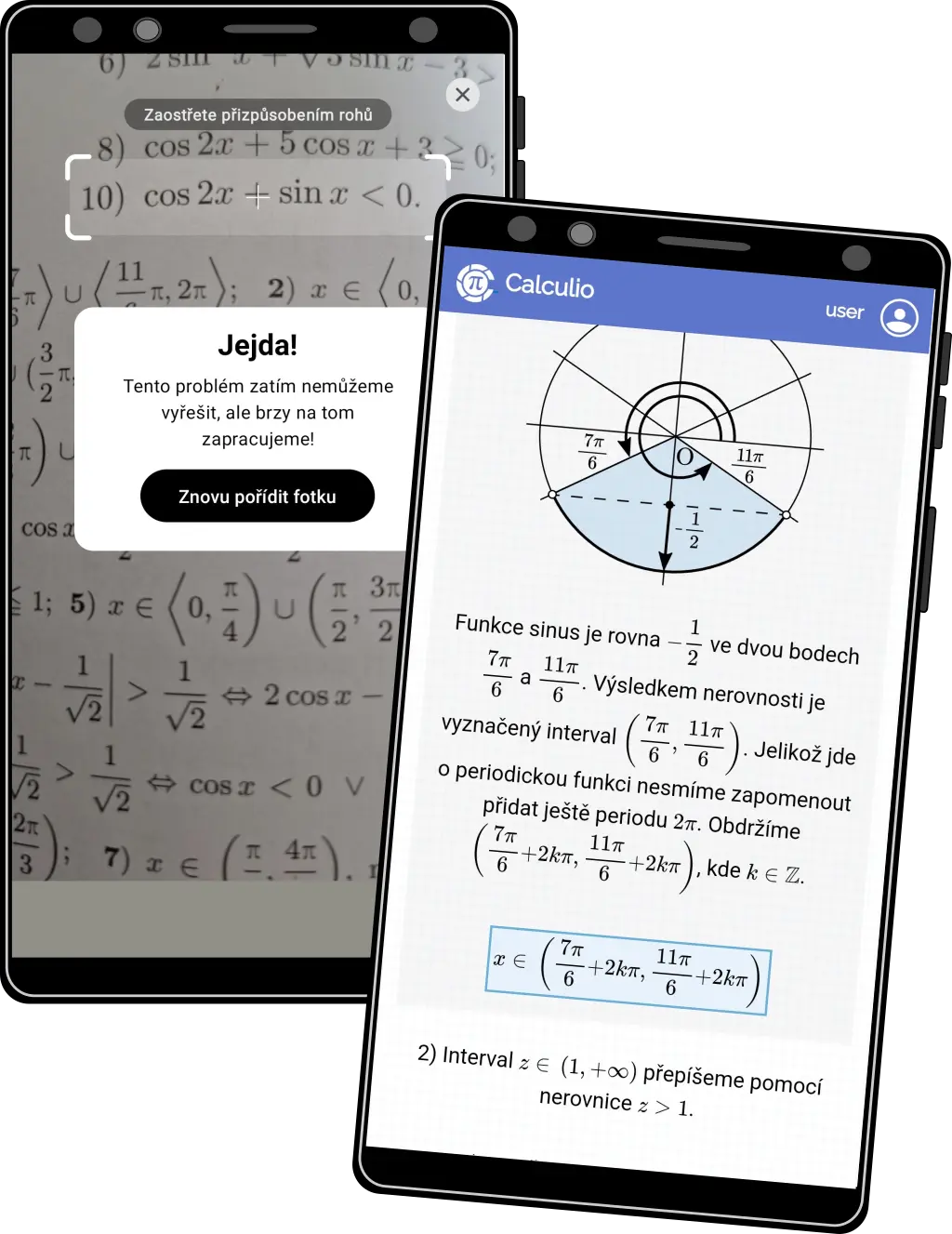
Goniometrické nerovnice
- Většina konkurenčních aplikací goniometrické nerovnice vůbec nezvládá
- Jde o složitější téma, které i přesto řešíme srozumitelnou formou.
- Rovněž využíváme grafickou reprezentaci jednotkové kružnice
- Na obrázku vlevo Photomath, vpravo Calculio
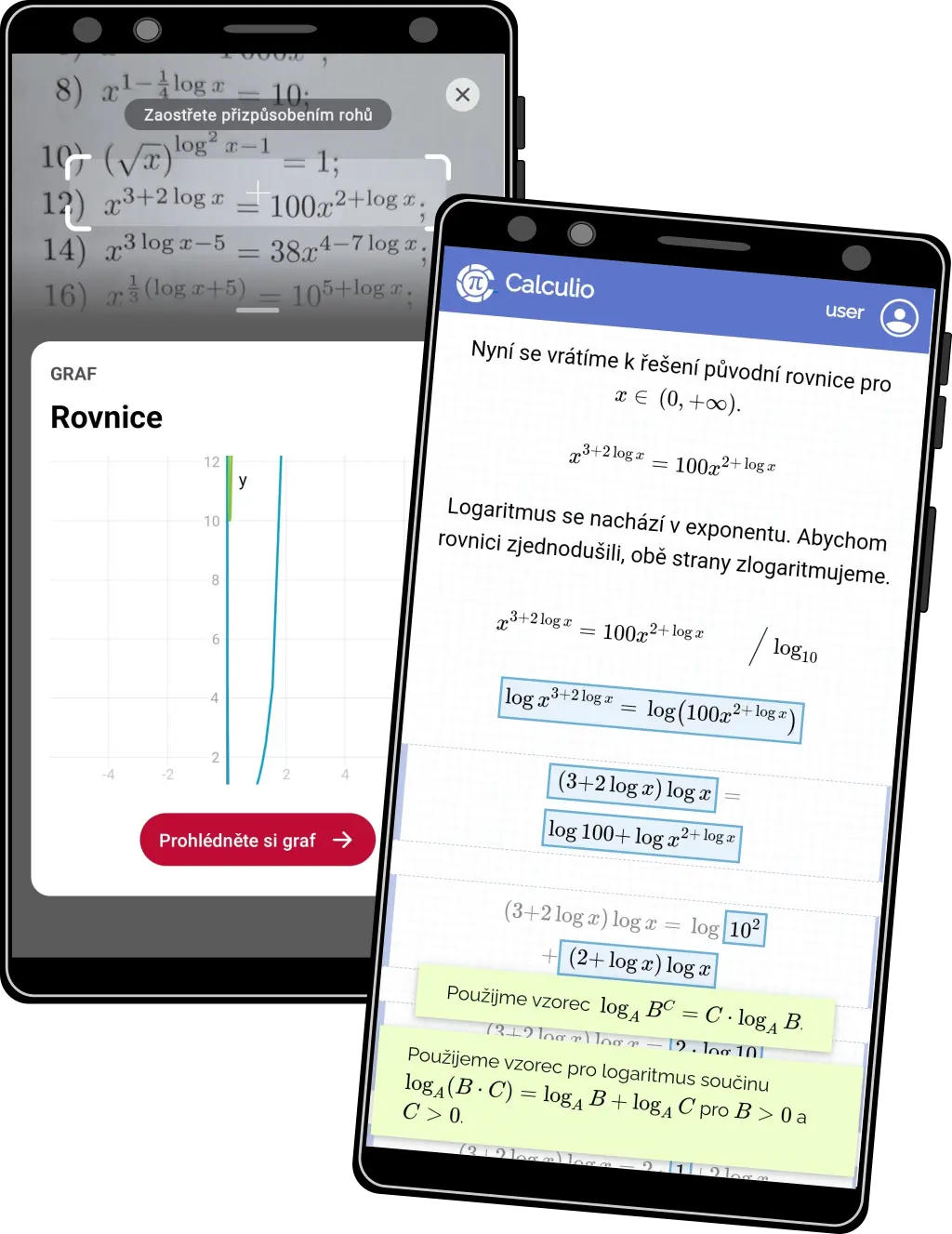
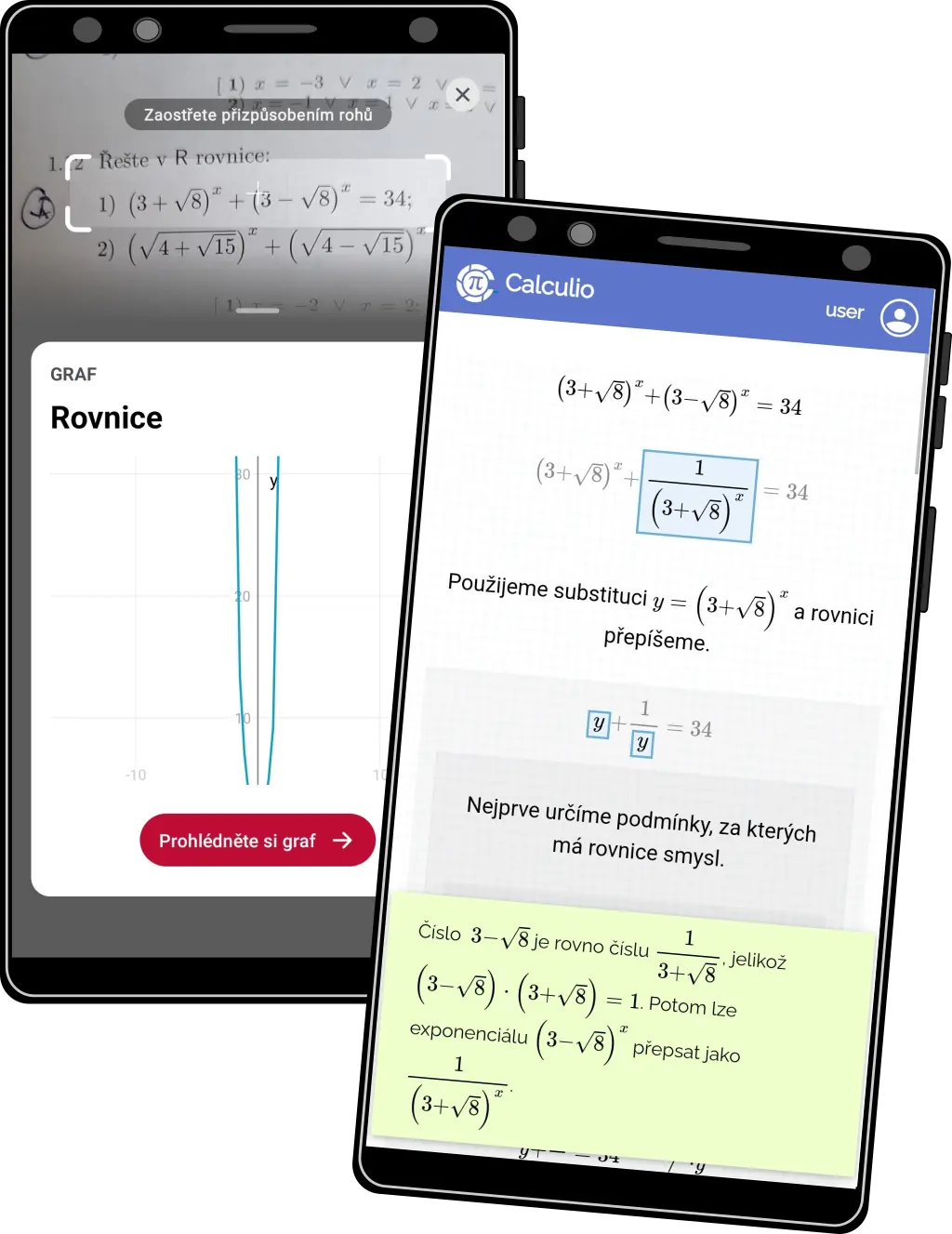
Exponenciální a logaritmické rovnice #1
- Přehlednou a srozumitelnou formou umíme řešit tyto typy rovnic a nerovnic
- Zvládáme i složité rovnice.
- Na obrázku vlevo Photomath, vpravo Calculio
Exponenciální a logaritmické rovnice #2
- Ukážeme vám běžně používané "finty" k řešení složitějších úloh ve sbírkách a učebnicích.
- Na obrázku vlevo Photomath, vpravo Calculio
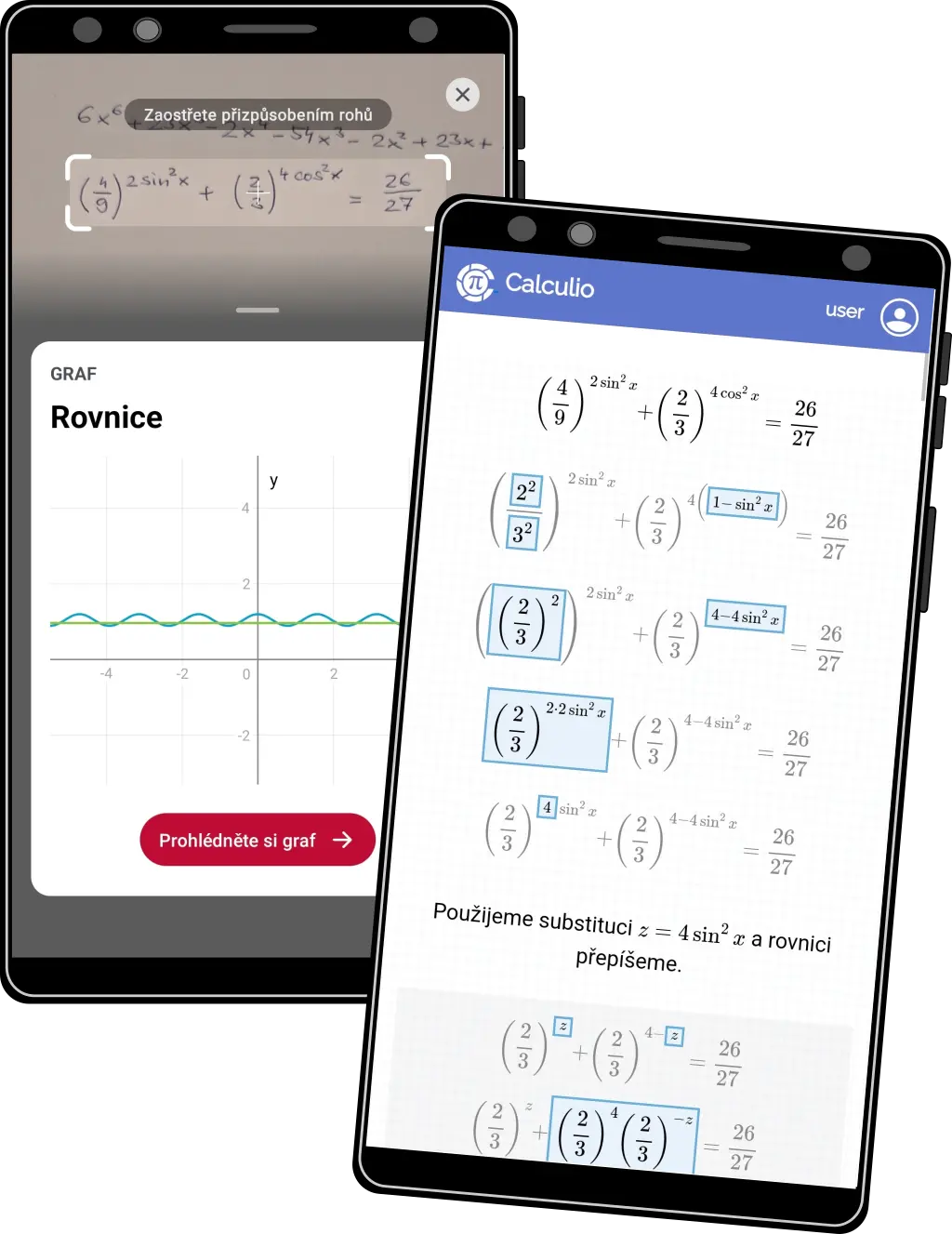
Exponenciální a logaritmické rovnice #3
- Nezastaví nás ani kombinace složitých témat jako jsou exponenciální rovnice kombinované s goniometrickými výrazy.
- Na obrázku vlevo Photomath, vpravo Calculio
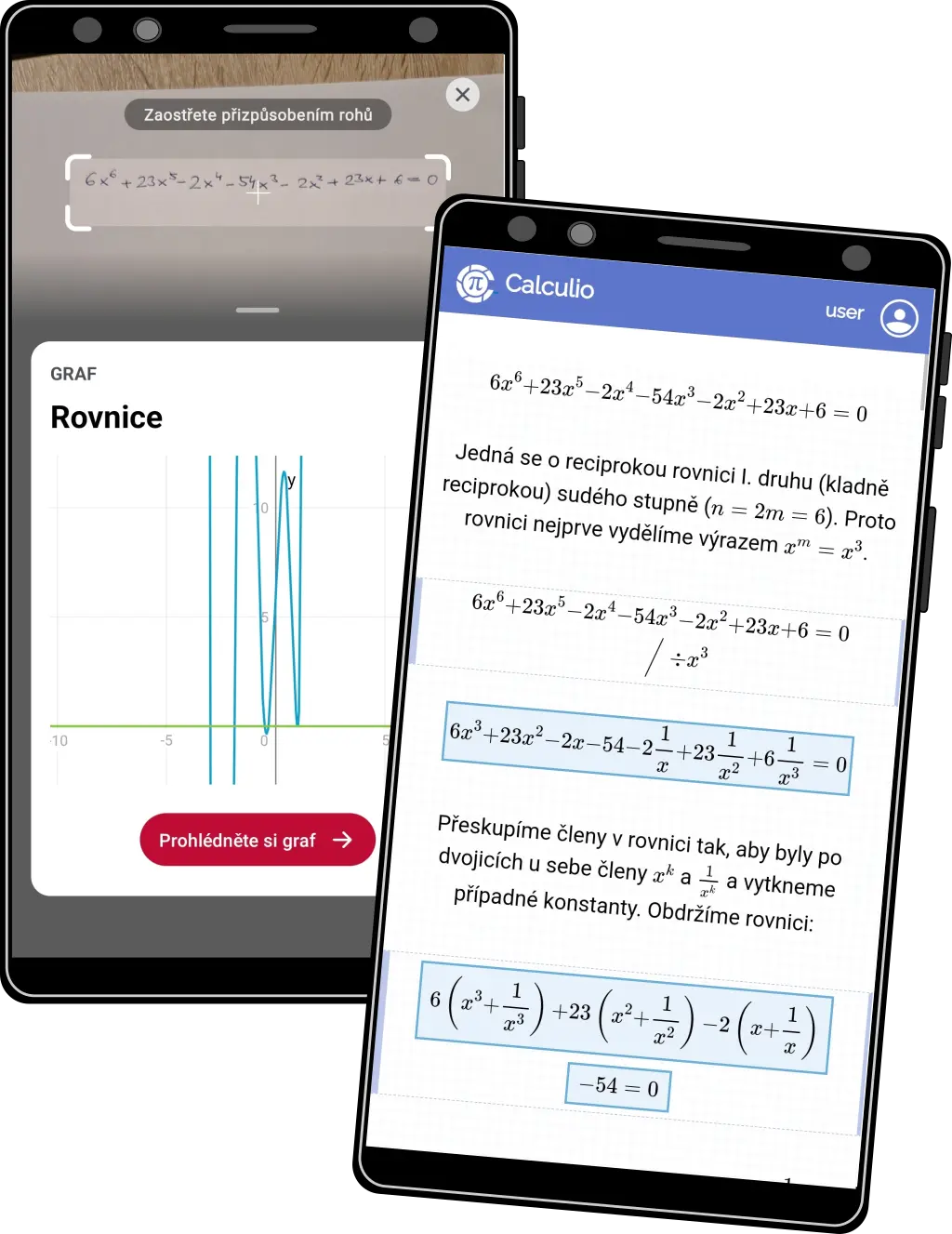
Reciproké rovnice
- Běžně probírané téma na středních školách.
- Poskytneme řešení přehlednou a srozumitelnou formou
- Na obrázku vlevo Photomath, vpravo Calculio
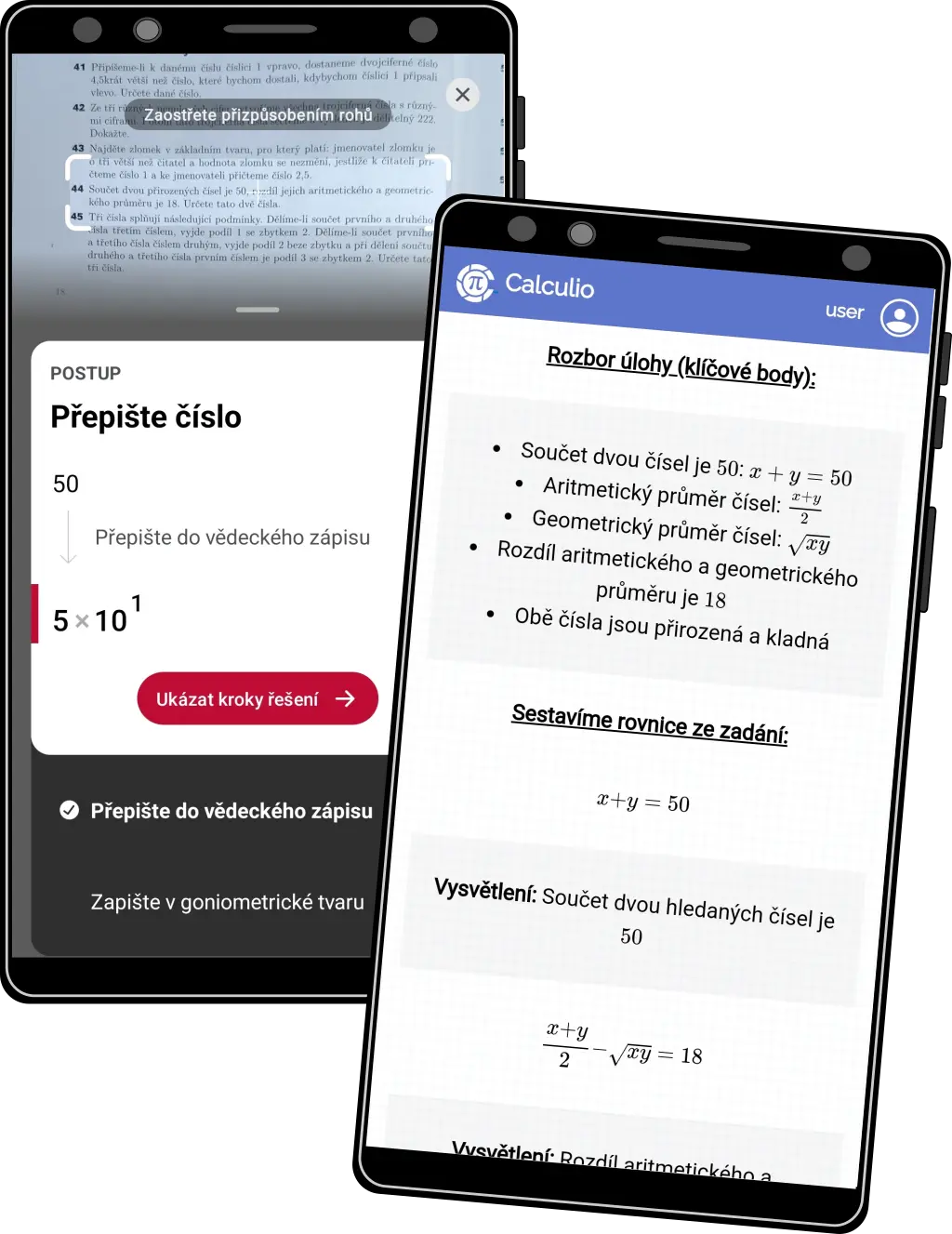
Slovní úlohy
- Podporujeme řešení slovních úloh vedoucích k rovnicím. Více informací zde
- Na obrázku vlevo Photomath, vpravo Calculio
Úprava výrazů #1
- Dokážeme usměrnit i relativně složité výrazy
- Na obrázku vlevo Photomath, vpravo Calculio
Úprava výrazů #2
- Elegantně zjednodušíme i číselné goniometrické výrazy
- Na obrázku vlevo Photomath, vpravo Calculio
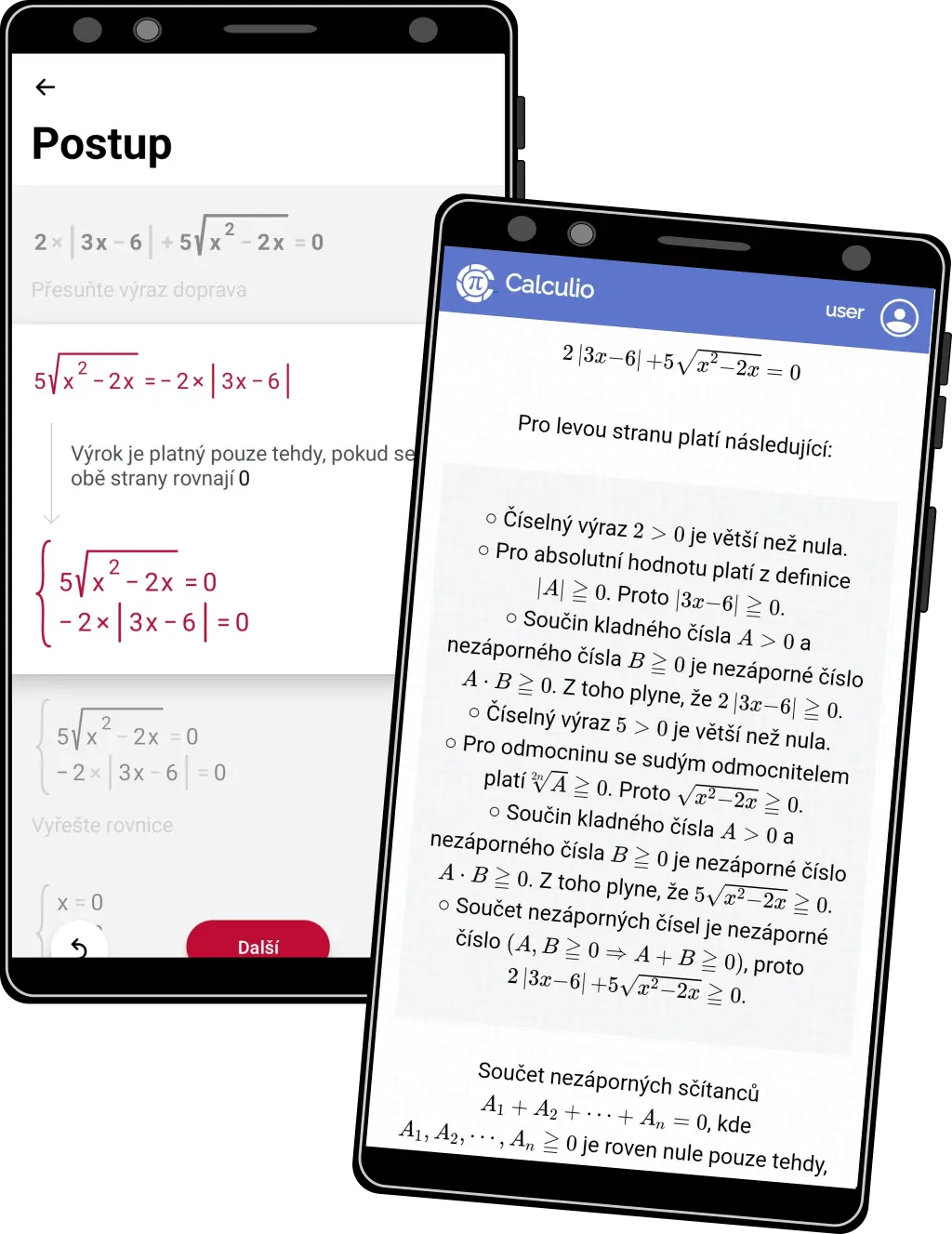
Dedukce #1
- Využíváme různé dedukce, které usnadňují výpočet. V arzenálu jich máme desítky.
- Do detailu vysvětlíme co, jak a hlavně PROČ jsme udělali.
- Zde je ukázáno, že součet nezáporných sčítanců je roven nule pouze tehdy, pokud je každý sčítanec roven nule
- Na obrázku vlevo Photomath, vpravo Calculio
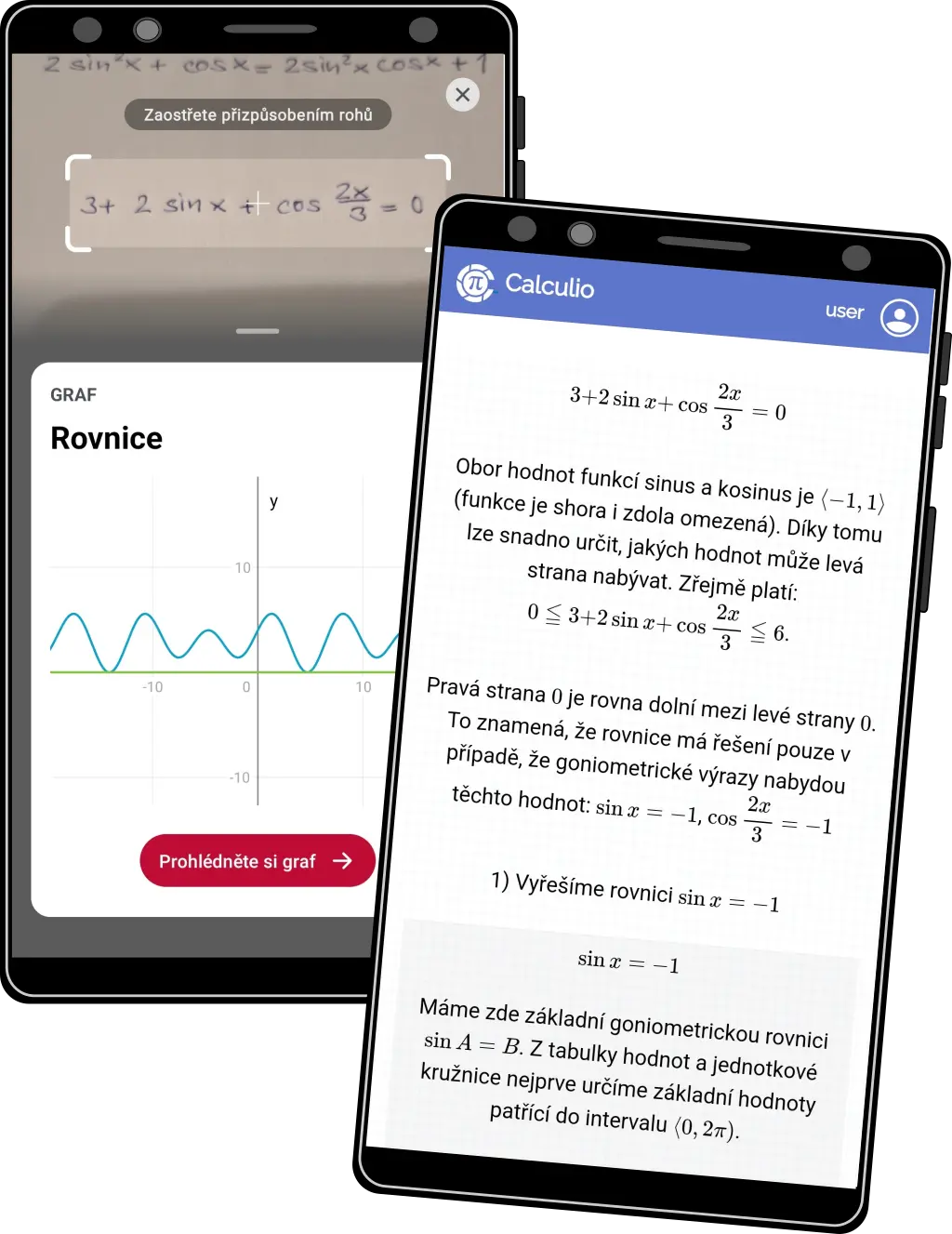
Dedukce #2
- Ukázka dedukce na základě oboru hodnot funkcí.
- Na obrázku vlevo Photomath, vpravo Calculio